الهندسة في الحضارات المختلفة
الهندسة عند الاغريق
** يرجع الفضل لتقدم الاغريق في الهندسة إلى طاليس حيث استطاع أن يحدد
ارتفاع الهرم من خلال قياس طول ظله.
** وكان فيثاغورس هو أول من طبع الهندسة بطابعها الحالي المنطقي، كما كان
أول من رتب النظريات الأساسية ترتيباً منطقياً منظماً.
**
في عام 450 ق.م. بدأت تظهر سلسلة من النظريات المبنية على بعض مسلمات وتعريفات
معروضة عرضاً منطقياً متصلاً. ومن أشهر هذه النظريات كان ماقدمه اقليدس.
نظام أقليدس الهندسي يتكون من:
** مجموعة من المصطلحات غير المعرفة.
**
مجموعة من التعريفات .
**
مجوعة من المسلمات والمبادئ العامة.
** نظام منطقي لتحديد صحة أو عدم صحة القضايا الجديدة.
** سلسلة من القضايا تسمى نظريات.
التعاريف:
** النقطة: هي ما ليس له أجزاء.
**
الخط: هو طول بلا عرض.
**
طرفي الخط: عبارة عن نقط.
** الخط المستقيم: هو ما يقع تماماً على نقاطه.
** السطح: هو ما له طول وعرض فقط.
** أطراف السطح: عبارة عن خطوط.
** السطح المستوي: هو سطح يقع تماماً على خطوطه المستقيمة.
** الزاوية المستوية: هي ميل خطين متقابلين مستويين بالنسبة لبعضهما وبحيث
لا يقعان معاً في خط مستقيم واحد.
**
الزاوية المستقيمة: عندما يقع الخطان المكونان للزاوية على نفس الخط المستقيم فإن
الزاوية تسمى زاوية مستقيمة الخطين.
** الزاوية القائمة: عندما يقام أحد ضلعي الزاوية على خط مستقيم مكوناً
زاويتين متجاورتين متساويتين فإن كلاً من الزاويتين المتساويتين تسمى زاوية قائمة.
** الدائرة: شكل مستو محتوى بخط واحد يسمى المحيط . بحيث أن كل الخطوط
المستقيمة المرسومة من نقطة معينة داخل الشكل إلى المحيط تكون متساوية.
** المستقيمات المتوازية: هي المستقيمات التي تقع في نفس المستوى والتي إذا
ما مدت من أي جهتيها فإنها لاتلتقي في أي من الجهتين مهما امتدت.
المسلمات:
بنى اقليدس أصوله على خمس مسلمات هي:
**
يمكن رسم خط مستقيم من أي نقطة إلى أخرى.
**
يمكن مد خط مستقيم محدود باستمرار كخط مستقيم.
** يمكن رسم دائرة بمعلومية مركز ومسافة معلومة.
** الزاويا القائمة متطابقة.
** إذا قطع مستقيم مستقيمين بحيث أن مجموع الزاويتين الداخليتين وفي جهة
واحدة من القاطع تكون أقل من قائمتين. فإن هذين المستقيمين يلتقيان اذا مدا على
استقامتهما من هذه الجهة التي يكون فيها مجموع الزاويتين الداخلتين اقل من
قائمتين.
يمكن تلخيص المسلمتان (1) ، (2) معاً في المسلمة التالية: أي نقطتين يحددان
خطاً مستقيماً واحداً وأن الخط المستقيم يمتد امتداداً لا نهائياً.
المسلمة (3) تنص على: الدائرة تتعين بمعلومية مركزها ونصف قطرها.
من ثم يمكن تصنيف مسلمات اقليدس الخمسة الى:
مسلمات الوجود (1، 2، 3) وفيها افترض وجود مبادئ اساسية.
مسلمات خواص هندسية (4، 5) وفيها افترض توفر خواص هندسية معينة لبعض
الأشكال.
المبادئ العامة:
وضع اقليدس مجموعة من المبادئ العامة منها:
**
الأشياء المساوية لنفس الشئ تكون متساوية.
**
إذا أضيفت متساويات إلى متساويات كانت النتائج متساوية.
** الأشياء المتطابقة مع بعضها تكون متساوية.
** الكل أكبر من الجزء.
النظريات:
بعد وضع الأساس قام اقليدس بتكوين البناء الهندسي للأصول والذي يشتمل على
الخواص الهندسية، التي قام بالبرهنة عليها مراعياً ما يأتي:
**
كل عبارة (علاقة هندسية) جديدة لابد من اثبات صحتها بالبرهان.
**
كل مصطلح جديد ينبغي تعريفه، وأكثر من ذلك ينبغي التدليل على وجوده.
الكتاب الأول :
تضمن 48 نظرية.
تناولت هذه النظريات تطابق
المثلثات، المستقيمات المتوازية، المساحات.
تضمن نظرية فيثاغورس وعكسها.
برهن اقليدس على الـثمانية
وعشرون الأولى استناداً على المسلمات الأربعة الأولى.
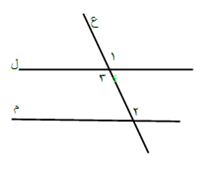
النظرية (27):
إذا قطع مستقيم مستقيمين
بحيث كانت الزاويتان المتبادلتان متساويتان كان مستقيمان متوازيين.
المعطيات:
ع مستقيم يقطع المستقيمين ل، م.
المطلوب: اثبات أن المستقيم ل // المستقيم م.
استخدم اقليدس في برهان هذه النظرية البرهان غير المباشر.
حيث افترض أن ل و م يتقابلان في النقطة د .
وبالتالي فإن هذا يتناقض مع النظرية 16 في كتابه والتي تنص على ” الزاوية
الخارجة للمثلث أكبر من أي زاوية أخرى ماعدا المجاورة لها“
نظرية (28):
إذا قطع مستقيم مستقيمين ، فإن المستقيمين يكونان متوازيين إذا تحقق واحد
من الشرطين التاليين:
* تساوت أي زاويتين متناظرتين.
*
كان مجموع زاويتين داخليتين في جهة واحدة من القاطع يساوي قائمتين.
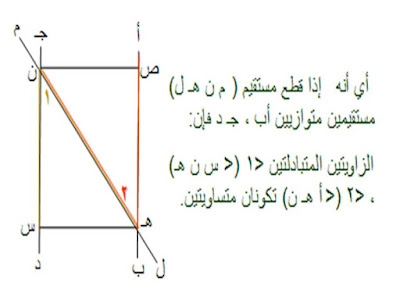
إذا قطع مستقيم مستقيمين ، فإن المستقيمين يكونان متوازيين إذا تساوت أي
زاويتين متناظرتين.
المعطيات:
ع مستقيم يقطع المستقيمين ل، م.
<1 = <2
المطلوب: اثبات أن المستقيم ل // المستقيم م.
استخدم اقليدس في برهان هذه النظرية النظرية 15 في كتابه .
والتي تنص على تساوي الزاويتين المتقابلتين في الرأس.
وبالتالي فإن <1 = <3. ،
ومن المعطيات يكون <2 =<3
وحيث أنهما زاويتيين متبادلتين
يكون ووفقاً للنظرية 27 ل // م
==== إذا قطع مستقيم مستقيمين ، فإن المستقيمين يكونان متوازيين إذا كان
مجموع زاويتين داخليتين في جهة واحدة من القاطع يساوي قائمتين.
المعطيات: ع مستقيم يقطع المستقيمين ل، م.
<4 + <3 = 2ق
المطلوب: اثبات أن المستقيم ل // المستقيم م.
استخدم اقليدس في برهان هذه النظرية النظرية 13 في كتابه .
والتي بناءً عليها يكون <4 + <3 = 2ق.
وحيث أن <2 = <3 يكون
<4 + <2 = 2ق
ووفقاً للنظرية 27 يكون
المستقيم ل // المستقيم م
النظرية (29):
إذا قطع مستقيم مستقيمين متوازيين فإن:
*
الزوايا المتبادلة تكون متساوية.
* الزوايا المتناظرة تكون متساوية.
* مجموع الزاويتين الداخليتين في جهة واحدة من القاطع تساوي قائمتين.
استخدم اقليدس ولأول مرة المسلمة الخامسة في برهان هذه النظرية.
ومن هنا ظهرت اشكالية المسلمة الخامسة.
اشكالية المسلمة الخامسة
المسلمة 5 تنص
على:
إذا قطع مستقيم مستقيمين
بحيث أن مجموع الزاويتين الداخليتين وفي جهة واحدة من القاطع تكون أقل من قائمتين.
فإن هذين المستقيمين يلتقيان اذا مدا على استقامتهما من هذه الجهة التي يكون فيها
مجموع الزاويتين الداخلتين اقل من قائمتين.
النظرية 28 تنص على:
إذا قطع مستقيم مستقيمين ،
فإن المستقيمين يكونان متوازيين إذا تحقق واحد من الشرطين التاليين:
تساوت أي زاويتين متناظرتين.
* كان مجموع زاويتين داخليتين في جهة واحدة من القاطع يساوي قائمتين.
لاحظ: المسلمة الخامسة هي معكوس النظرية 28
من هنا جاء التشكك في هذه المسلمة . وقالوا لماذا لم يشتق اقليدس هذه
المسلمة كنظرية وقام بالبرهنة عليها.
وقد حاول الكثير من الرياضيين البرهنة على هذه المسلمة كمبرهنة من بين هذه
المحاولات كانت محاولات :
وبعد أن برهن الخيام النظريات الثمانية ذكر بأن هذا هو البرهان الحقيقي
لنظرية المتوازيات وبذلك يكون قد أكمل النقص في البناء الرياضي لاقليدس.
العودة للصحة الرئيسة
العودة للصحة الرئيسة













ليست هناك تعليقات:
إرسال تعليق